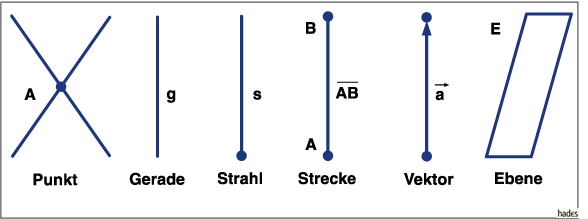
|
|
|
|
|
|
|
|
Äquivalent zu den Zahlen in der Arithmetik dienen Punkt, Gerade, Ebene und Winkel in der Geometrie als Grundelemente:
Punkt (
), dimensionslos, ohne Ausdehnung:
Schnittpunkt zweier Linien.
Linie, eindimensionale Punktmenge: Verschiebung (Translation)
eines Punktes oder Schnitt zweier Ebenen.
Gekrümmte Linien
(Kurven, Kreislinien, Parabeln,
Hyperbeln, Kurven höherer Ordnung) oder
gerade Linien.
Gerade (g), beidseitig unbegrenzte gerade Linie.
Strahl (s), einseitig begrenzte gerade Linie.
Strecke (
), beidseitig begrenzte gerade Linie,
Strecke zwischen Punkt A und Punkt B.
Vektor (
, Strecke mit
Richtungssinn.
Bezeichnung durch seinen Anfangs- und Endpunkt und einen
darübergesetzten Pfeil oder durch einen (kleinen oder großen)
fetten Buchstaben 
, manchmal wird auch
die Schreibweise 
verwendet.
Ebene, zweidimensionale Punktmenge, entsteht bei Verschiebung einer Geraden längs einer anderen, nicht parallelen Geraden, Begrenzung von bestimmten Körpern, den Polyedern (Keil, Würfel usw.).
Das folgende Bild zeigt die Grundelemente der ebenen Geometrie
Winkel (
), entsteht durch
Drehung ( Rotation) eines Strahls um einen Punkt,
den Scheitelpunkt; mißt den
Richtungsunterschied zweier Strahlen. Auch: Verhältnis
des Kreisbogens der Drehung zum Radius (Bogenmaß).
Drehsinn, mathematisch positiver Drehwinkel: Drehsinn im Gegenuhrzeigersinn (,,links herum``); mathematisch negativer Drehwinkel: Drehung im Uhrzeigersinn (,,rechts herum``).
|
|
|
|
|
|
|
|
