|
|
|
|
|
|
|
|
eindeutig festgelegt (
). B-Splines bilden eine Basis
für den Vektorraum der Spline-Funktionen auf dem Gitter 
;
jede Spline-Funktion kann daher als Linearkombination von B-Splines
geschrieben werden:
Tatsächlich gilt für 
:
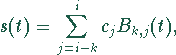
da 
für 
.
Die Definition und Berechnung der B-Splines erfolgt rekursiv:
Dabei ist
Die so definierten B-Splines 
sind auf dem Intervall
sogar positiv und bilden
eine Zerlegung der Eins
auf 
:
B-Splines finden z.B. Anwendung als Ansatzfunktionen (Testfunktionen)
bei eindimensionalen Finite-Element-Rechnungen.
|
|
|
|
|
|
|
|
