|
|
|
|
|
|
|
|
heißt konvergent, wenn es einen
Wert a gibt, für den gilt:
Für eine beliebig vorgegebene Zahl 
existiert ein Index 
,
so daß alle Glieder mit 
einen Abstand von 
haben,
der kleiner ist als 
:
a heißt Grenzwert der Folge.
Darstellung:
ist eine konvergente Folge mit dem
Grenzwert 
.
Eine nicht konvergente Folge heißt divergent.
Nullfolge, Folge mit dem Grenzwert Null.
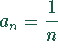ist eine Nullfolge.
Cauchy-Folge, Folge, für die zu jeder beliebig vorgegebenen Zahl
ein Index 
existiert, so daß alle Glieder
mit 
einen Abstand voneinander haben, der kleiner
ist als 
:
Im Reellen (und Komplexen) ist jede Cauchy-Folge konvergent.
Jede nach oben (unten) beschränkte,
monoton steigende (fallende) Folge ist konvergent.
Der Grenzwert ist das Supremum (Infimum).
|
|
|
|
|
|
|
|
