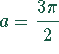|
|
|
|
|
|
|
|
kann wie man der vorhergehenden Abbildung
entnimmt, mehrere Werte a
besitzen (in Wirklichkeit unendlich viele).
kann z.B. durch die Bögen 
und
beschrieben werden.
vergrößert werden, die Funktionen sind periodisch.
kann durch die Bögen
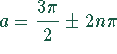, beschrieben werden.
Funktionen mit großem Argument
(d.h. nach der Addition von vielen Umläufen) werden auf
Computern und Taschenrechnern meist mit schlechterer Genauigkeit
berechnet als Funktionen mit kleinem Argument.
Die Zuordnungsfunktionen heißen Sinusfunktion, Cosinusfunktion und Tangensfunktion (um den Funktionscharakter zu verdeutlichen wird x anstelle von a verwendet).
Weitere trigonometrischen Funktionen sind die Sekansfunktion,
, die Cosekansfunktion, 
, und die
Cotangensfunktion, 
, welche die
reziproken Funktionen zu Sinus, Cosinus und Tangens sind.
Die Rückzuordnung von s, c und t nach a ist nicht mehr eindeutig!
Um Mehrdeutigkeit zu vermeiden, legt man einen sogenannten Hauptwert fest.
Näheres wird dazu im Zusammenhang mit den Arkusfunktionen
erläutert.
Zwei wichtige Relationen der trigonometrischen Funktionen wurden
schon dargestellt:
|
|
|
|
|
|
|
|
