|
|
|
|
|
|
|
|
QR-Zerlegung, die Vektoren 
und 
des n-dimensionalen Raumes werden als
Spalten einer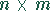 
-Matrix A bzw. Q aufgefaßt. Das
Orthogonalisierungsverfahren entspricht der Aufgabe, für eine gegebene
-Matrix A eine orthogonale Matrix Q zu finden,
so daß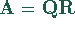 
für eine geeignete rechte obere
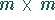-Dreiecksmatrix R ist.
QR-Zerlegungen spielen eine zentrale Rolle in
der Ausgleichsrechnung und bei Eigenwertproblemen. Geeignete Verfahren zur
QR-Zerlegung sind das Cholesky-Verfahren für
symmetrische, positiv definite Matrizen, das Householder-Verfahren und das Gram-Schmidt-Verfahren.
|
|
|
|
|
|
|
|
