|
|
|
|
|
|
|
|
gleich der transponierten Matrix 
ist.
Die Eigenwerte orthogonaler Matrizen haben den Absolutwert
Eins.
Die Eigenvektoren 
einer symmetrischen Matrix 
können als
Spaltenvektoren einer orthogonalen Matrix 
aufgefaßt werden, mit
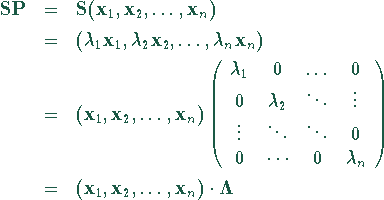
mit der Diagonalmatrix 
, deren Diagonalelemente die Eigenwerte
von 
sind:
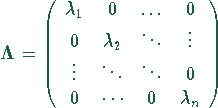
Diagonalisierung von 
:
Das Produkt aller Eigenwerte von 
ist gleich dem Absolutglied des
charakteristischen Polynoms
|
|
|
|
|
|
|
|
