|
|
|
|
|
|
|
|
Gauß-Jordan-Verfahren, mit elementaren Umformungen wird das lineare Gleichungssystem
schrittweise in die Diagonalform des äquivalenten Gleichungssystems
übergeführt, mit denselben Lösungen wie das ursprüngliche Gleichungssystem!
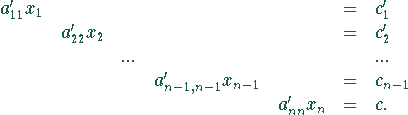
Die Unbekannten in den Gleichungen werden so reduziert, daß
in jeder Gleichung nur noch eine Unbekannte vorkommt.
Umformung des Gleichungssystems auf Diagonalform:
In n Eliminationsschritten berechnet man die neuen Koeffizienten des
k-ten Schritts, 
, rekursiv:
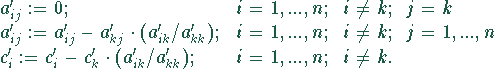
Lösungen 
in Diagonalform:
Lösungen der 
sind direkt ablesbar, wenn im k-ten
Eliminationsschritt die k-te Zeile normiert wird.
Im Unterschied zum Gauß-Verfahren werden im
Gauß-Jordan-Verfahren die Unbekannten während des
Eliminationsschrittes auch von den darüberliegenden Zeilen eliminiert.
Normierung der Gleichungen mittels Division durch die
Diagonalelemente (Diagonalmatrix wird zur Einheitsmatrix).
Darstellung des umgeformten Gleichungssystems 
in Matrixschreibweise:
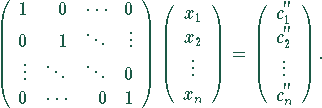
Direktes Ablesen des Lösungsvektors 
des Gleichungssystems:
|
|
|
|
|
|
|
|
