|
|
|
|
|
|
|
|
Lineare Gleichungssysteme mit großen, schwach besetzten Matrizen sollten eher mit iterativen Methoden gelöst werden.
Gaußsches Eliminationsverfahren:
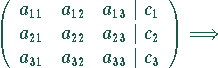
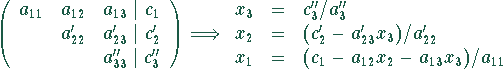
Gauß-Jordan (Matrixinversion):
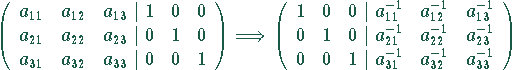
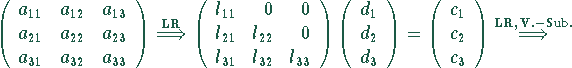
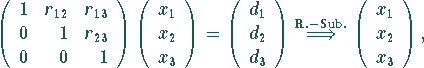
wobei V.-Sub. Vorwärtssubstitution nach 
bedeutet, R.-Sub.
Rückwärtssubstitution nach 
und LR die LR-Zerlegung.
Gauß-Seidel-Methode:
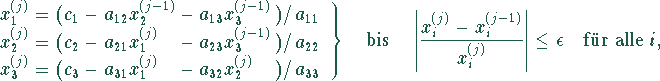
wobei j die j-te Iteration ist und 
eine vorgegebene
Genauigkeitsschranke. (Diese Genauigkeitsangabe gilt nur für numerisch
gutartige Matrizen.)
|
|
|
|
|
|
|
|
