|
|
|
|
|
|
|
|
links-rechts), im englischen
LU (lower-upper-decomposition), Zerlegung einer Matrix 
in ein Produkt einer rechten Dreiecksmatrix 
mit einer linken
Dreiecksmatrix 
, basierend auf dem Gauß-Verfahren.
Jede Matrix 
, bei der für die Durchführung des Gauß-Algorithmus
keine Pivotisierung erforderlich ist, kann als Produkt einer linken unteren
und einer rechten oberen Dreiecksmatrix geschrieben werden:
Nicht jede Matrix besitzt eine LR-Zerlegung.
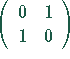besitzt keine LR-Zerlegung.
Algorithmus zur Lösung des Gleichungssystems
1. Schritt: LR-Zerlegung der Koeffizientenmatrix 
2. Schritt:
Einführung eines (unbekannten) Hilfsvektors 
und
Lösung des linearen Gleichungssystems 
:
3. Schritt: Lösung des Gleichungssystems
:
Die LR-Zerlegung ist dann zu empfehlen, wenn mehrere lineare
Gleichungssysteme mit gleicher Koeffizientenmatrix A aber
jeweils verschiedener Inhomogenität c zu lösen sind; Schritt 1
ist dann nur einmal durchzuführen.
Die Zerlegung der Koeffizientenmatrix 
in die linke
Dreiecksmatrix 
und die rechte Dreiecksmatrix 
ist nicht eindeutig. Die wichtigsten Zerlegungen, basierend
auf der Gaußelimination,
sind die Doolittle-, die Crout- und die Cholesky-Zerlegung.
|
|
|
|
|
|
|
|
