|
|
|
|
|
|
|
|
trivialerweise gegen
. Ansonsten braucht sie nicht konvergent zu sein. Auch bei
Konvergenz muß der Grenzwert nicht gleich dem Funktionswert 
sein,
wie das folgende Beispiel zeigt.
Die Funktion
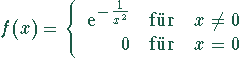
ist unendlich oft differenzierbar mit 
für alle n. Die
Taylor-Reihe mit der Entwicklungsstelle 
konvergiert damit
für alle x gegen den Wert 
.
Konvergenz der Taylor-Reihe gegen den entsprechenden Wert 
,
wenn für das Restglied gilt:
Man sagt in diesem Fall, daß 
durch seine Taylor-Reihe
dargestellt wird.
Funktion zweier Variablen:
Taylor-Reihenentwicklung einer Funktion 
von zwei Variablen
an der Stelle 
, 
:
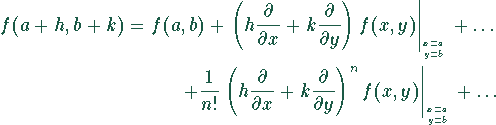
mit
etc.
|
|
|
|
|
|
|
|
