|
|
|
|
|
|
|
|
const., 
const.
Die homogene lineare Differentialgleichung 2. Ordnung mit konstanten
Koeffizienten ist in jedem Fall durch den Ansatz 
lösbar. Es treten drei mögliche Fälle auf:
:
:
:
Die Lösung der inhomogenen Gleichung erfolgt nach der oben
erläuterten Methode.
:
:
:
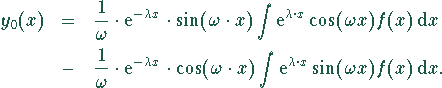
Da die auftretenden Integrale stets vom Typ 
bzw. 
, 
sind, kann man für viele Störglieder 
die Lösungen
mit Hilfe der Laplace-Transformation finden.
|
|
|
|
|
|
|
|
