Lineare Differentialgleichungen mit konstanten Koeffizienten
Wie in der Einleitung gezeigt, lassen sich mit Hilfe der Laplace-Transformation
spezielle Lösungen linearer Differentialgleichungen mit konstanten
Koeffizienten finden. Die aus drei Schritten bestehende Prozedur ist
schematisch dargestellt:
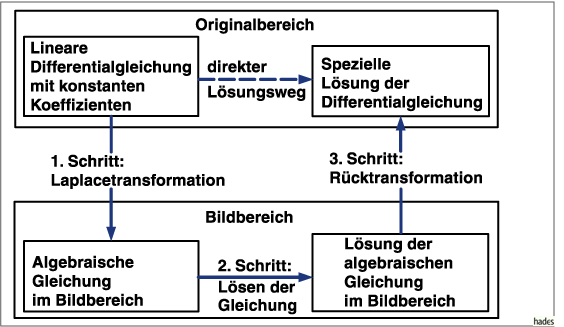
Die für lineare Differentialgleichungen 1. und 2. Ordnung mit konstanten
Koeffizienten beschriebenen Methoden können mit
Hilfe des Differentiationssatzes auf Differentialgleichungen höherer
Ordnung verallgemeinert werden.
