|
|
|
|
|
|
|
|
Ansatz:
Einsetzen:
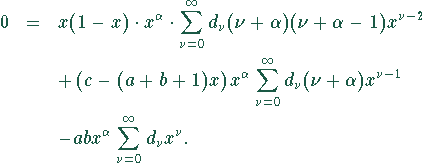
Es folgt:
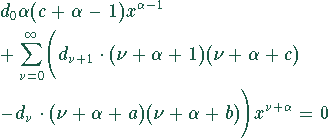
Koeffizientenvergleich liefert die Indexgleichung:
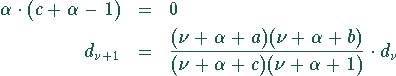
Dies ergibt:
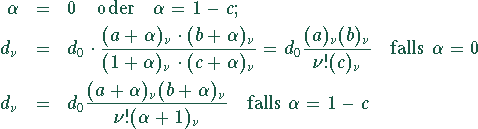
mit 
.
Damit folgt:
wobei 
die hypergeometrische Funktion
bezeichnet. Die allgemeine Lösung der Gaußschen
Differentialgleichung lautet damit
Die zweite Lösung gilt nur für den Fall 
. Falls 
ist, existiert ebenfalls eine
Lösung, diese hat aber eine viel kompliziertere Gestalt.
|
|
|
|
|
|
|
|
