|
|
|
|
|
|
|
|
Diese Systeme sind von der Gestalt:
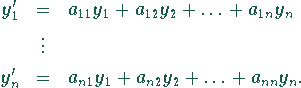
Ansatz: 
.
Einsetzen:
Also
Nichttriviale Lösungen gibt es nur, wenn
.
Charakteristisches Polynom,
das Polynom, das durch Ausmultiplizieren der Gleichung
entsteht.
Dies gibt ein Polynom vom Grad n für 
, das n (im
allgemeinen komplexe) Nullstellen
hat. Sind diese Nullstellen paarweise verschieden, so bilden die
Vektoren
eine Basis des Lösungsraumes. Die einzelnen Koeffizientenvektoren
bestimmen sich durch Einsetzen in die
entsprechende Gleichung.
d.h.
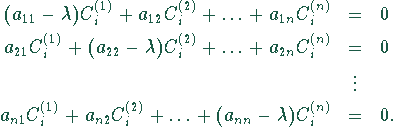
Die allgemeine Lösung lautet damit:
wobei die 
aus den Anfangsbedingungen bestimmt werden müssen.
|
|
|
|
|
|
|
|
