|
|
|
|
|
|
|
|
ist
in verschiedenen Koordinatensystemen dargestellt
worden. In Kugelkoordinaten
(
) gilt:
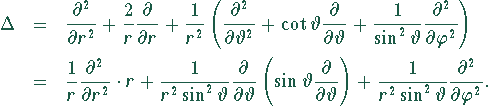
Die Laplacegleichung 
lautet
daher:
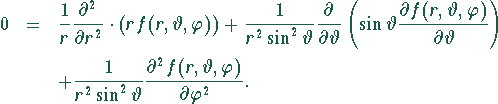
Separationsansatz: 
Also:
Somit:
Nochmalige Separation: 
Also
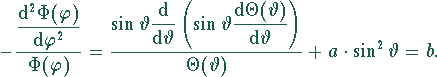
Somit
Da man fordern muß 
(die Lösung soll eindeutig sein), folgt 
, d.h.
, 
,
Setzt man nun 
(das ist
immer möglich), so
folgt
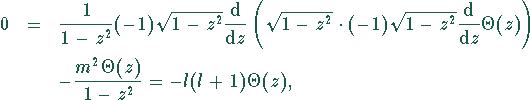
d.h.
Für 
ist dies genau die Legendresche Differentialgleichung.
Die Differentialgleichung für 
heißt
zugeordnete Legendresche Differentialgleichung, ihre Lösungen
sind die zugeordneten Legendrepolynome. Diese sind aus den
gewöhnlichen Legendrepolynomen berechenbar gemäß
Somit:
Normierung:
Man setzt:
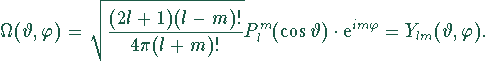
sind die Kugelflächenfunktionen.
Radialgleichung:
Ansatz: 
; dies liefert 
, d.h. 
oder 
.
Damit gilt:
|
|
|
|
|
|
|
|
