|
|
|
|
|
|
|
|
Bild- und Urbildmenge brauchen nicht identisch zu sein, z.B. kann
ein Operator ein skalares Feld auf ein Vektorfeld abbilden oder umgekehrt.
ordnet
jeder Funktion 
ihre Ableitung 
zu.
Partieller Ableitungsoperator 
leitet eine Funktion 
mehrerer Veränderlicher nach einer Variable y ab.
Die anderen Variablen
werden als Konstanten behandelt.Nabla-Operator, formal ein Vektor, dessen entsprechende Komponenten die partiellen Ableitungsoperatoren bilden:
Mehrfache partielle Ableitung, mehrfache Ausführung des partiellen Ableitungsoperators:
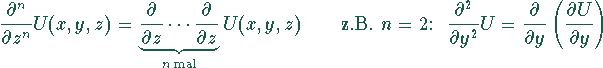
ergibt die n-te Ableitung von U. Laplace-Operator, das Skalarprodukt des Nabla-Operators mit sich selbst; Summe über alle partiellen zweiten Ableitungen:
Der Laplace-Operator ist ein Skalar und kein Vektor.
Gemischte partielle Ableitung, Nacheinanderausführung von
partiellen Ableitungen nach verschiedenen Komponenten.
Ist die abzuleitende Funktion 
zweifach stetig partiell differenzierbar,
so kann die Reihenfolge der Ableitungen vertauscht werden, z.B.
Biharmonischer Operator,
zweifache Ausführung des Laplace-Operators.
|
|
|
|
|
|
|
|
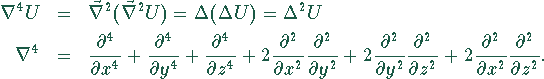
