|
|
|
|
|
|
|
|
Hypergeometrische Verteilung, gibt die Wahrscheinlichkeit, mit der aus einer Gesamtmenge N unter n Stichproben k fehlerhafte Proben zu finden sind.
Ausschußzahl, Anzahl fehlerhafter Stücke (bekannt)
.
Schlechtanteil ( Ausschuß) p, Anteil fehlerhafter Teile an der
Gesamtmenge.
Im Sinn eines Prüfverfahrens kann die
Bedingung Ausschußzahl 
als Hypothese und
p als der Schätzparameter der
Wahrscheinlichkeitsverteilung
aufgefaßt werden.
Aussagesicherheit, Annahmewahrscheinlichkeit
, gibt die
Wahrscheinlichkeit an, weniger oder genau k Fehlerproben zu finden
(Wahrscheinlichkeitssumme):
Mit der Wahrscheinlichkeit 
ist es richtig,
eine Sendung nicht anzunehmen, sobald die Anzahl der fehlerhaften
Teile in der Stichprobe 
ist!
Bei sehr großen Stückzahlen (
) kann auch die
Poisson-Verteilung verwendet werden.
AQL-Wert (Acceptable Quality Level),
ein in Absprache zwischen Kunden und Hersteller
festgesetzter Wert für 
(gewöhnlich
), mit dem bei einer Stichprobenzahl n höchstens k
Fehler zugelassen werden.
Mit fallendem Schlechtanteil p der Gesamtmenge steigt natürlich
die Annahmewahrscheinlichkeit. Der Hersteller wird versuchen,
möglichst weit unter den zur Berechnung des AQL-Wertes
verwendeten Ausschußwert 
zu bleiben.
Der AQL-Wert ist das Signifikanzniveau der Ausschußprüfung,
siehe Prüfverfahren.
Annahmekennlinie, Abbildung des
Fehleranteils in der Gesamtmenge 
auf die
Annahmewahrscheinlichkeit 
bei vorgegebenem Stichprobenumfang n und maximaler
Anzahl von Ausschußteilen k in der Stichprobe.
Ist der AQL-Wert für 
vorgegeben, lassen sich der
notwendige Stichprobenumfang n und die maximal zulässige Anzahl
der Ausschußteile 
an der jeweiligen Kennlinie ablesen.
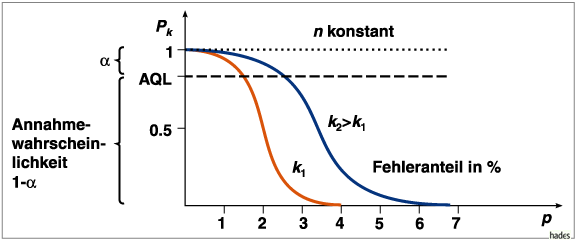
Als Beispiel sind in dem folgenden Bild zwei Kennlinien
zu einem Stichprobenumfang, aber unterschiedlichen
Werten für die maximal erlaubte Anzahl fehlerhafter Elemente
und 
aufgetragen.
|
|
|
|
|
|
|
|
