|
|
|
|
|
|
|
|
Punktschätzung, Schätzung eines Wertes für eine Stichprobenfunktion durch Entnahme einer Stichprobe.
Stichprobenfunktion, Abbildung von n Stichproben 
auf einen Wert 
, Zufallsgröße der
Stichprobe.
Einfache Beispiele sind die Anzahl fehlerhafter Teile
pro Tag in der Herstellung von Gütern oder der Mittelwert einer
Meßreihe einer physikalischen Größe.
Beispiele für Stichprobenfunktionen sind i.allg.
Schätz- und Prüffunktionen.
Schätzfunktion ,
Schätzer , Abbildung von n Stichproben auf einen
Schätzwert
für einen
Parameter W einer angenommenen Verteilung,
Spezialfall einer Stichprobenfunktion.
Beispiele für Schätzfunktionen sind das arithmetische
Mittel einer Stichprobe mit Umfang n
und die empirische Varianz
Realisation einer Schätzfunktion,
Wert einer Schätzfunktion nach der Entnahme einer Stichprobe.
Losziehung, Würfeln, Entnahme einer Stichprobe, Aufnahme einer
Meßreihe usw.
Erwartungstreue Schätzfunktion, Schätzfunktion,
deren Erwartungswert
bei mehreren Stichproben tatsächlich durch den Wert des gesuchten
Parameters gegeben ist.
Mediantreue Schätzfunktion , Schätzfunktion mit gleichen Wahrscheinlichkeiten für die Unterschätzung und die Überschätzung
Einfach konsistente Schätzfunktion,
Schätzfunktion, für die
bei beliebig kleinem 
(
) gilt
d.h., für 
strebt der aus einer Stichprobe ermittelte
Wert 
gegen den tatsächlichen Parameterwert W, die
Varianz (Streuung) geht gegen Null, 
.
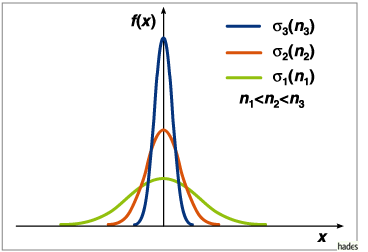
Das arithmetische Mittel 
der Stichprobe aus einer
normalverteilten
Gesamtheit strebt zum Beispiel gegen den Erwartungswert m einer
Normalverteilung.
|
|
|
|
|
|
|
|
