|
|
|
|
|
|
|
|
Konsistenz im mittleren Fehlerquadrat impliziert einfache
Konsistenz, jedoch ist der umgekehrte Schluß nicht notwendig wahr!
Mittlerer quadratischer Fehler
von 
, 
Effizienz, von zwei erwartungstreuen Schätzfunktionen 
und 
ist diejenige effizienter bzw. wirksamer, deren
Varianz bei vorgegebenem Stichprobenumfang n kleiner ist
d.h., die erwartete Streuung um den wahren Wert W ist geringer.
Absolut effiziente, wirksamste Schätzfunktion, Schätzfunktion mit der kleinsten Varianz.
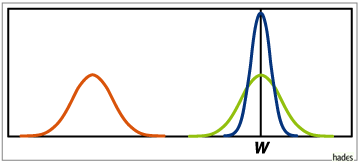
durchgezogen: absolut effizient, punktiert:
erwartungstreu, gestrichelt: nicht erwartungstreu
Ungleichung von Rao und Cramer, ist 
irgendeine
Schätzfunktion für den Verteilungsparameter W und die
Gesamtheit 
- bzw. 
-verteilt, so gilt:
wobei x stetig, sonst ist
wobei x diskret.
Suffizienz, eine Schätzfunktion ist suffizient, wenn
sie die gesamte Information der n Stichproben 
berücksichtigt.
Die wenigsten Schätzer sind suffizient. Beispielsweise
ist der Median
nicht suffizient, da er nur den Wert in der Mitte einer
geordneten Stichprobe berücksichtigt.
Schätzer, die durch die Maximum-Likelihood-Methode
berechnet werden, sind suffizient.
Faktorisierungskriterium, für die Suffizienz ist das
folgende Kriterium hinreichend und notwendig
,
d.h., die Wahrscheinlichkeit für eine spezielle
Stichprobenkonfiguration 
ist das Produkt
aus der von dem Parameter W abhängigen
Wahrscheinlichkeitsverteilung
der Schätzfunktion g und einer parameterunabhängigen
Verteilung
der Stichprobenkonfiguration.
BAN ( bester asymptotisch normalverteilter Schätzer),
Schätzfunktion 
für den Parameter W mit der Eigenschaft,
daß 
für große n (
) gegen eine Normalverteilung
konvergiert
mit 
und der Varianzuntergrenze nach Rao-Cramer.
Maximum-Likelihood-Schätzer sind BAN-Schätzer.
BLU ( bester linear unverzerrter Schätzer),
Schätzfunktion 
für den Parameter W, die erwartungstreu,
absolut effizient (geringste Varianz)
und eine lineare Funktion der 
ist.
|
|
|
|
|
|
|
|
