|
|
|
|
|
|
|
|
, die eine Auswahl von
zweidimensionalen
Meßpunkten (Meßkurve) 
optimal beschreiben.
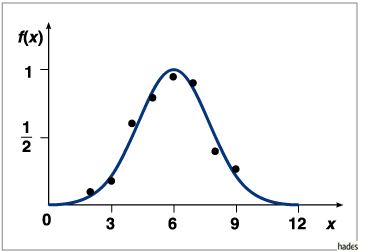
Minimalprinzip der kleinsten Quadrate nach Gauß,
bei vorgegebenem Funktionsansatz 
(Ansatzfunktion)
und n vorgegebenen Wertepaaren 
ist
die optimale Parameterkonfiguration der Ansatzfunktion definiert durch
wobei a der Parameter des Ansatzes ist.
Kleinstquadratschätzer, löst man die Normalgleichungen des Minimalprinzips, erhält man Schätzfunktionen für die Parameter des Funktionsansatzes.
Eigenschaften für linearen Ansatz der Schätzfunktion/Schätzgerade,
- linear und erwartungstreu.
|
|
|
|
|
|
|
|
