|
|
|
|
|
|
|
|
-Funktion, Funktion zur Bestimmung des bestmöglichen
Parameterwertes bei vorgegebener Art der Verteilung;
mit einer
Stichprobe vom Umfang n werden die Stichprobenvariablen 
in einer Tabelle der relativen Häufigkeiten 
mit vorgegebener Klassifizierung 
zusammengefaßt; die 
-Funktion lautet dann
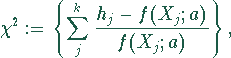
wobei 
die Intervallmitte der j-ten Klasse darstellt.
Die 
-Funktion ist ein Maß für die Abweichung
der relativen Häufigkeitsverteilung 
von einer
idealen Verteilung 
zu gegebenem Parameterwert a.
Für diskrete Meßwerte entfällt i.allg. die Einteilung
in Klassen,
an Stelle der Intervallmitten werden die Meßwerte
eingesetzt.
-Minimumprinzip, Anwendung der
Methode der kleinsten Quadrate
zur Bestimmung der
statistischen Verteilung von Meßwerten;
das Minimum der 
-Funktion bezüglich der Variablen a
definiert analog zum Maximum-Likelihood-Schätzer den Parameterschätzwert 
und damit
die Schätzfunktion 
bei
vorgegbener Art der Verteilung 
Das 
-Verfahren kann auch bei
Maximum-Likelihood-Verteilungen,
die von mehreren Parametern 
abhängen, eingesetzt werden.
Auch bei Prüfverfahren, in
denen selbst die Art der Verteilung unbekannt ist,
wird die 
-Methode verwendet.
Asymptotisch (für großen Stichprobenumfang n)
stimmt die 
-Schätzfunktion mit dem Maximum-Likelihood-Schätzer
überein.
|
|
|
|
|
|
|
|
