Integration durch Spline-Interpolation
Zur Integration einer Funktion, die nur durch eine Wertetabelle 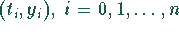 definiert ist,
kann man wie folgt vorgehen:
definiert ist,
kann man wie folgt vorgehen:
Diese Wahl der Randbedingungen stellt sicher, daß die Methode Polynome bis zum Grad 3 exakt integriert.
program Integration2(input, output);
{Integration durch Splines}
uses
stdfile;
const
MaxArray = 255;
type
MyArray = array[0..MaxArray] of double;
var
t, y: MyArray;
x: double;
n, i: integer;
h0, h1: double;
a, b: double;
u, v, w: MyArray;
nd, hd: MyArray;
c: MyArray;
q: double;
h, res: double;
procedure init;
var
fName: string;
f: text;
begin {init}
writeln('Integration durch Splines');
writeln;
writeln('Welche Datei enthaelt die Punktepaare? (In integr2.dat liegt ein Beispiel.)');
readln(fName);
if StdOpen(f, fName) then begin
n := -1;
repeat
n := n + 1;
if n > MaxArray then begin
writeln('Die Datei "', fName, '" hat zu viele ',
'Stuetzstellen (mehr als ', MaxArray, ').');
halt
end {if}
until not StdRead2(f, t[n], y[n]);
n := n - 1
end else begin {if}
writeln('Kann Datei "', fName, '" nicht oeffnen.');
halt
end; {if}
close(f);
writeln('Insgesamt ', n + 1, ' Stuetzstellen gelesen.');
writeln
end; {init}
procedure Randbedingungen(var c: MyArray; u, v, w, y, t: MyArray);
var
h1, hn, h2, hm: double;
d1, dn, d2, dm: double;
b1, b2: double;
alpha, beta: double;
a11, a12, a21, a22: double;
det: double;
i: integer;
begin {Randbedingungen}
h1 := t[1] - t[0];
hn := t[n] - t[n - 1];
d1 := (y[1] - y[0]) / h1;
dn := (y[n] - y[n - 1]) / hn;
b1 := 3 * d1 - u[1];
b2 := 3 * dn - u[n - 1];
h2 := t[2] - t[1];
hm := t[n - 1] - t[n - 2];
d2 := (y[2] - y[1]) / h1;
dm := (y[n - 1] - y[n - 2]) / hm;
a11 := (v[1] + 1) / sqr(h1) - (v[1] + v[2]) / sqr(h2);
a12 := w[1] / sqr(h1) - (w[1] + w[2]) / sqr(h2);
b1 := (u[1] + u[2] - 2 * d2) / sqr(h2) - (u[1] - 2 * d1) / sqr(h1);
a21 := (v[n - 1] + v[n - 2]) / sqr(hm) - v[n - 1] / sqr(hn);
a22 := (w[n - 1] + w[n - 2]) / sqr(hm) - (1 + w[n - 1]) / sqr(hn);
det := a11 * a22 - a12 * a21;
b2 := (2 * dm - u[n - 1] - u[n - 2]) / sqr(hm) + (u[n - 1] - 2 * dn) /sqr(hn);
alpha := (b1 * a22 - a12 * b2) / det;
beta := (a11 * b2 - b1 * a21) / det;
c[0] := alpha;
for i := 1 to n - 1 do begin
c[i] := u[i] + alpha * v[i] + beta * w[i]
end; {for}
c[n] := beta
end; {Randbedingungen}
function Spline(x: double; t, y, c: MyArray): double;
var
k: integer;
h, delta: double;
a0, a1, a2, a3: double;
begin {Spline}
k := n + 1;
repeat
k := k - 1
until (x > t[k]) or (k = 0);
k := k + 1;
h := t[k] - t[k - 1];
delta := (y[k] - y[k - 1]) / h;
a0 := y[k];
a1 := c[k];
a2 := (c[k] - delta) / h;
a3 := (c[k] - 2 * delta + c[k - 1]) / sqr(h);
Spline := ((a3 * (x - t[k - 1]) + a2) * (x - t[k]) + a1) * (x- t[k]) + a0
end; {Spline}
procedure result;
begin {result}
writeln('Das Integral liefert den Wert ', res:8:4)
end; {result}
begin {Splines}
init;
h0 := t[1] - t[0];
a := (y[1] - y[0]) / sqr(h0);
v[1] := -1 / h0;
for i := 1 to n - 1 do begin
h1 := t[i + 1] - t[i];
b := (y[i + 1] - y[i]) / sqr(h1);
u[i] := 3 * (a + b);
hd[i] := 2 * (1 / h0 + 1 / h1);
nd[i] := 1 / h1;
a := b;
h0 := h1
end; {for}
w[n - 1] := -1 / h1;
{Vorwaertselimination}
for i := 1 to n - 2 do begin
q := -nd[i] / hd[i];
hd[i + 1] := hd[i + 1] + nd[i] * q;
u[i + 1] := u[i + 1] + q * u[i];
v[i + 1] := q * v[i]
end; {for}
{Rueckwaertselimination}
for i := n - 1 to 2 do begin
q := hd[i];
u[i] := u[i] / q;
v[i] := v[i] / q;
w[i] := w[i] / q;
q := nd[i - 1];
u[i - 1] := u[i - 1] - q * u[i];
v[i - 1] := v[i - 1] - q * v[i];
w[i - 1] := -q * w[i]
end; {for}
q := hd[1];
u[1] := u[1] / q;
v[1] := v[1] / q;
w[1] := w[1] / q;
Randbedingungen(c, u, v, w, y, t);
res := 0;
for i := 1 to n do begin
h := t[i] - t[i - 1];
res := res + h / 6 * (y[i - 1] + 4 * Spline(t[i - 1] + h/2, t, y, c) + y[i])
end; {for}
result
end. {Integration2}















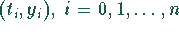 definiert ist,
kann man wie folgt vorgehen:
definiert ist,
kann man wie folgt vorgehen:
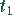 und
und  sein soll.
sein soll.







