|
|
|
|
|
|
|
|
Die hier verwendeten Rechenoperationen werden im Abschnitt Rechnen mit reellen
Zahlen definiert.
Addition, Multiplikation und Potenzieren von natürlichen Zahlen
n und m, (
) ergeben
jeweils wieder eine natürliche Zahl:
Die Subtraktion 
(Umkehrung der Addition) hingegen führt u.U. aus 
heraus,
.
Die Division 
(Umkehrung der Multiplikation) führt u.U. ebenfalls aus 
heraus,
.
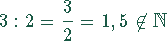Läßt sich eine natürliche Zahl m ohne Rest durch eine andere
natürliche Zahl n teilen, so ist n Teiler von m. m ist
durch n teilbar.
Gleichzeitig ist m Vielfaches von n.
21 hat die Teiler 1,3,7,21.
Eins ist Teiler jeder natürlichen Zahl,
jede natürliche Zahl hat sich selbst zum Teiler und
jede natürliche Zahl ist Teiler von Null.
Ist m Teiler von k und n Teiler von m, so ist auch
n Teiler von k.
3 ist Teiler von 6; 6 ist Teiler von 24, also ist auch 3 Teiler von 24.
In PASCAL sind spezielle INTEGER Divisionen möglich:
n div m , 
gibt die größte natürliche Zahl l mit 
,
n mod m gibt den Rest, der bei der Division 
bleibt.
In FORTRAN wird bei Division von INTEGER -Größen automatisch
der Divisionsrest abgeschnitten, d.h. n/m in FORTRAN entspricht
n div m in PASCAL.
7 div 3 = 2 und
7 mod 3 = 1.
|
|
|
|
|
|
|
|
