|
|
|
|
|
|
|
|
Als Padé-Approximation 
bezeichnet man die gebrochen
rationale Funktion
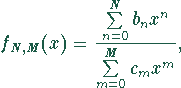
deren Taylor-Entwicklung um 
mit der Potenzreihe von f bis
einschließlich der 
-ten Potenz übereinstimmt. Im Gegensatz zur
Taylor-Reihenentwicklung lassen sich für die Padé-Approximationen
keine allgemeingültigen Konvergenzregeln für 
(Restgliedabschätzung) angeben.
O.B.d.A. kann man 
annehmen, andernfalls dividiert man
Zähler und Nenner durch 
.
Je nach Wahl von N und M kann man verschiedene
Padé-Approximationen konstruieren, die die Funktion bis zur
-ten Potenz approximieren.
Nach Vorgabe von N und M bestimmt man die Padé-Approximation
wie folgt:
Aus der Bedingung, daß 
die Funktion 
bis zur
Ordnung 
approximieren soll, erhält man zwei Gleichungssysteme
zur Bestimmung der Koeffizienten 
und 
:
Dabei soll gelten, daß 
für 
.
Mit 
lautet die erste Gleichung in Matrixform:
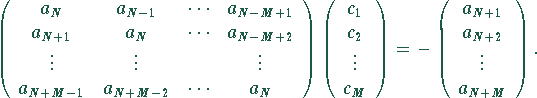
Daraus lassen sich (z.B. durch Elimination nach Gauß)
die Koeffizienten 
bestimmen. Aus
der zweiten Gleichung erhält man dann die Koeffizienten 
:
Die beiden letzten Gleichungen bezeichnet man als
Padé-Gleichungen. Mit der Kenntnis der Entwicklungskoeffizienten
und 
ist 
vollständig bestimmt.
|
|
|
|
|
|
|
|
