|
|
|
|
|
|
|
|
Der Pol liegt in einem Brennpunkt des Kegelschnitts, 
ist
der Winkel zwischen dem Radiusvektor und der Verbindungslinie von diesem
Brennpunkt zum nächstliegenden Scheitelpunkt. Diese Gleichung
erfaßt nur einen Ast der Hyperbel.
Implizite Gleichung in kartesischen Koordinaten:
Auflösen nach positiven y-Werten ergibt
Unterscheidung nach der Exzentrizität 
:
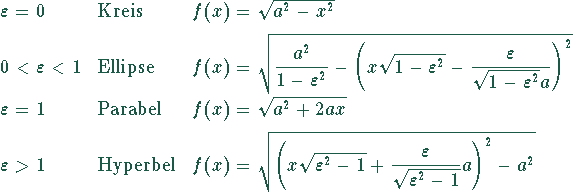
Die Umkehrfunktionen führen für 
auf die
Gleichung einer Parabel, für 
auf die Funktion
und für 
auf die auf der
y-Achse verschobene Hyperbel 
.
Analoge Betrachtungen können auch im drei- und höher
dimensionalen Raum gemacht werden, dabei entstehende Körper werden
Ellipsoide, Hyperboloide etc. genannt.
|
|
|
|
|
|
|
|
