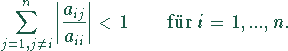
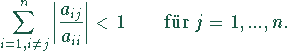
|
|
|
|
|
|
|
|
Kriterium von Schmidt - v.Mises:
Wenn der Betrag aller Diagonalelemente der Matrix 
groß gegen die Summe der restlichen Koeffizienten der
entsprechenden Zeilen oder Spalten ist, dann konvergieren die
Iterationsverfahren.
Wenn die Konvergenzkriterien nicht erfüllt sind, kann keine
Aussage gemacht werden, ob Konvergenz auftritt oder nicht, d.h. das
Verfahren kann unter Umständen trotzdem konvergieren!
Durch elementare Umformungen ist es manchmal möglich, ein
äquivalentes Gleichungssystem mit großen Diagonalelementen
herzustellen. Ist dies nicht möglich, muß die Lösung mit einem
direkten Verfahren ermittelt werden.
Thomas-Algorithmus für Tridiagonalmatrizen, Anwendung des Gauß-Algorithmus für spärlich besetzte Matrizen, bei dem die Rechenoperationen für die Nullelemente ausgespart werden.
|
|
|
|
|
|
|
|
