|
|
|
|
|
|
|
|
Bei großen Gleichungssystemen sind in der Praxis viele
Koeffizienten des Konstantenvektors 
und der
Systemmatrix 
gleich null.
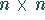-Matrix,
die Besetzungsdichte, d.h. die Anzahl der
Elemente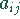 
, die nicht null sind, ist kleiner als
.
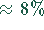Für einen Hochspannungsmast ergibt sich die
Matrixgleichung:
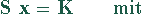
Bandbreite der Systemmatrix, die
Bandmatrix
enthält einen Streifen konstanter Breite, der mit Nichtnull-Elementen
besetzt ist.
|
|
|
|
|
|
|
|
