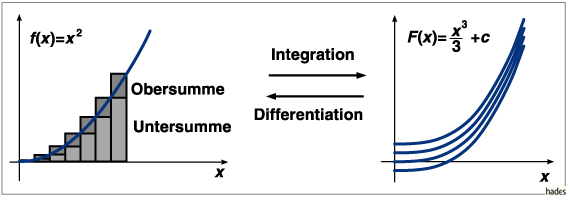
|
|
|
|
|
|
|
|
Ober-/Untersumme und Flächen über/unter der x-Achse
Berechnung einer Fläche:
Man zerlegt das Intervall 
in beliebige
Teilintervalle 
.
Sind 
und 
das Infimum und das Supremum der
Funktionswerte in dem Teilintervall i, dann definiert man als
Obersumme: 
die Flächeninhalte der Rechtecke, die alle über die Kurve ragen bzw.
unter der Kurve liegen.
Ober- und Untersummen können auch negativ sein,
wenn die Funktionswerte negativ sind.
Ober- bzw. Unterintegral,
bezeichnen die Grenzwerte der Ober- bzw.
Untersumme für unendlich viele Teilintervalle (falls sie
existieren).
Die Ober- bzw. Untersummen sind die Grundlagen der
numerischen Integration mit der Rechteckregel.
|
|
|
|
|
|
|
|
