|
|
|
|
|
|
|
|
,
Gleichheit der
Ober- und Unterintegrale
einer Funktion 
im Intervall 
.
Die Funktion 
ist integrierbar
im Intervall 
:
:
und 
und
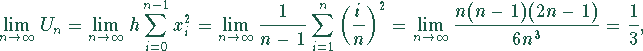
Unter- und Oberintegral sind gleich, d.h. 
ist
integrierbar.
Stetige Funktionen in einem abgeschlossenen Intervall
sind dort integrierbar.
, 
, 
, 
, 
, 
und
algebraische Ausdrücke von diesen sind integrierbar
(siehe ausführliche Tabellen).
Integrierbare Funktionen müssen nicht unbedingt stetig sein!
Beschränkte Funktionen mit endlich
vielen Sprüngen sind integrierbar.
Signum-Funktion
ist überall integrierbar.
Betragsfunktion 
ist überall integrierbar.
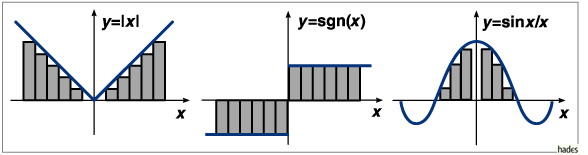
Integrierbare Funktionen mit Sprüngen/Knicken
Unbeschränkte Funktionen,
wie z.B. Funktionen mit Polstellen,
sind am Pol nicht integrierbar.
Bei solchen Funktionen darf die Integration nicht über
eine Polstelle laufen.
ist so nicht bestimmbar,
da 
bei 
eine Polstelle besitzt.
|
|
|
|
|
|
|
|
