|
|
|
|
|
|
|
|
Die Richtungsableitung eines Vektorfeldes in
Richtung des auf eins normierten Richtungsvektors 
ist
Verallgemeinert auf nicht normierte Vektoren 
, kann man
als Multiplikation der Richtungsableitung mit
dem Betrag a von 
darstellen.
In kartesischen Koordinaten 
läßt sich
schreiben:
Allgemein kann man schreiben
Vektorgradient, Operator 
, der jedem
Vektor 
den Vektor 
zuordnet.
Diese Zuordnung läßt sich in kartesischen Koordinaten als Multiplikation
eines Vektors mit einer Matrix beschreiben.
Der Vektorgradient kann demnach als Matrix (Tensor) dargestellt werden:
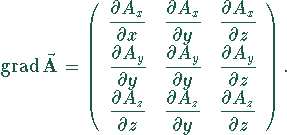
Er hat Bedeutung vor allem in der Elastizitätslehre im Maschinenbau (Spannungstensor, Dehnungstensor).
|
|
|
|
|
|
|
|
