|
|
|
|
|
|
|
|
Oft empfiehlt es sich, das Koordinatensystem zunächst durch eine
Rotation auf geeignete Achsen zu bringen.
Die Rotation um einen Winkel 
um die z-Achse transformiert
die Koordinaten 
in die gedrehten Koordinaten 
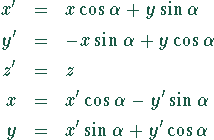
Analog kann auch um andere Achsen rotiert werden.
Meist bietet sich
durch die Aufgabenstellung (z.B. Richtung einer Dipolachse oder
einer Röhre) eine bestimmte Wahl der Achsen an.
Felder, die von Summen oder Differenzen von Koordinaten abhängen,
z.B.
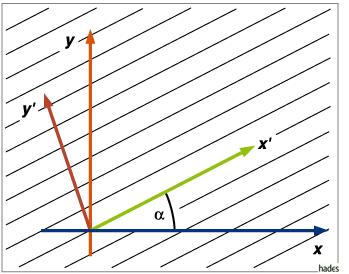
können so gedreht werden, daß sie nur noch von
einer Koordinate abhängen (siehe Figur).
Das Potential 
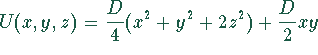läßt sich durch eine Drehung um 
mit den Transformationen
auf folgende Form bringen
Rotiert man nochmals um 
um die 
-Achse,
so wird 
, und man kann die Formel
für Zylinderkoordinaten 
benutzen:
Das ist das Potential eines zweidimensionalen harmonischen Oszillators.
Ebene Felder: Das Feld hängt nur von zwei Koordinaten (z.B.
) oder sogar von einer Koordinate ab (z.B. 
).
Gelingt eine solche Darstellung, so
vereinfacht das die Rechnung sehr, da Ableitungen nach der fehlenden
Koordinate zu Null werden.
Das Schwerefeld in der Nähe der Erdoberfläche ist eben.
Das Potentialfeld zwischen den Platten eines Kondensators ist eben.
|
|
|
|
|
|
|
|
