Sande-Tukey-Algorithmus: zweiter Schritt
Rekursion:
Aufspaltung in gerade und ungerade
Funktionen wird für die
Funktionen 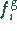 und
und  mit dem oberen Index
mit dem oberen Index  ) wiederholt.
Die durch weitere Wiederholungen definierte Rekursion ist beendet,
wenn der obere Index
) wiederholt.
Die durch weitere Wiederholungen definierte Rekursion ist beendet,
wenn der obere Index 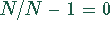 wird, wobei
die Fourier-Transformierte
wird, wobei
die Fourier-Transformierte  dann einfach der
Wert der Funktion
dann einfach der
Wert der Funktion 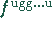 ist.
Falls die Beziehung zwischen der Reihenfolge der geraden (g) und
ungeraden (u)
Aufspaltungen der Funktion
ist.
Falls die Beziehung zwischen der Reihenfolge der geraden (g) und
ungeraden (u)
Aufspaltungen der Funktion  und der anfänglichen Reihenfolge der
diskreten Funktionswerte
und der anfänglichen Reihenfolge der
diskreten Funktionswerte 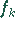 bekannt ist,
liefert dieses Rekursionsschema die
Fourier-Transformierte von
bekannt ist,
liefert dieses Rekursionsschema die
Fourier-Transformierte von  . Die gesuchte Beziehung ergibt sich
durch die Umkehr der Bitreihenfolge:
. Die gesuchte Beziehung ergibt sich
durch die Umkehr der Bitreihenfolge:
- Kehre zuerst die Reihenfolge der
geraden und ungeraden Aufspaltungen von
 in
in 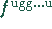 um:
um:

- Ordne dann g den Wert null zu und u den Wert eins.
- Das Ergebnis dieser Operation liefert für
jede Sequenz von geraden und
ungeraden Aufspaltungen von
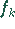 den Wert von k im Dualsystem.
den Wert von k im Dualsystem.
Damit ist
die Fourier-Transformierte bestimmt.

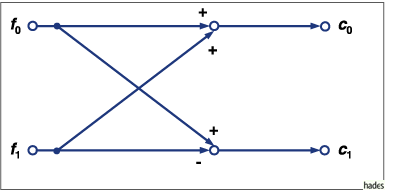
Symbolische Darstellung der FFT für die Reduktion von 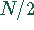 nach
nach 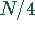 für die geraden Funktionen
für die geraden Funktionen 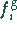
Symbolische Darstellung der FFT für 















![]()

![]() nach
nach ![]() für die geraden Funktionen
für die geraden Funktionen ![]()

![]()







