Differential- und Integralrechnung

Mathematica:

D[f[x],{x,n}]

liefert die n-te Ableitung der Funktion .

D[f,{x1,n1},{x2,n2},...]

liefert die gemischte (mehrfache) partielle Ableitung. Dt[f] erzeugt das vollständige Differential der Funktion f. Dt[f,x] liefert die vollständige Ableitung .

Maple:

>D[i](f);

der Operator der Differentiation, erzeugt die Ableitung der (Operator-)Funktion nach der i-ten Variablen.
 
D[i,j](f) ist äquivalent zu D[i](D[j](f)) und D[](f)=f .
 
>diff( Ausdruck,x1,x2,...,xn);

leitet den algebraischen Ausdruck partiell nach den Variablen ab.
 
Mehrfache Differentiation kann mit dem Folgenoperator $ dargestellt werden.
 
>diff(sin(x),x$5); äquivalent mit (diff(sin(x),x,x,x,x,x)) -> cos(x)

Unbestimmte Integrale:

Mathematica:

Integrate[f,x]

liefert das unbestimmte Integral ohne Integrationskonstante.

Maple:

>int(f,x) ;

(wie oben).
 
Es werden nur sehr wenige Integrale gefunden! Leider nicht einmal alle tabellierten.
 
Bestimmte Integrale, Mehrfachintegrale:

Mathematica

Integrate[f,{x,xa,xe}]

berechnet das bestimmte Integral der Funktion mit der unteren Grenze und der oberen Grenze .
 
In älteren Versionen als 2.2 berechnet Mathematica:

In[1]:=Integrate[1/xx{4,,-1,1}]
Out[1]=.

Ein Fehler, da das Integral uneigentlich ist!
 
Integrate[f[x,y],{x,xa,xe},{y,ya,ye}] , bestimmt das Zweifachintegral zunächst über y, danach über x.
 
Die Grenzen und können Funktionen von x sein.
 
Numerische Integration, erfolgt mit der Anweisung NIntegrate . Anders als bei der symbolischen Methode wird hier mit einer Datenliste gearbeitet.

MinRecursion und MaxRecursion , die minimale bzw. maximale Anzahl der Rekursionsschritte, mit denen in problematischen Bereichen (z. B. Polstellen) gerechnet wird (Voreinstellung 0 und 6).

In[1]:=NIntegrate[Exp[-xx{2],,-1000,1000}]

erzeugt wegen des sehr großen Integrationsbereichs und der ,,Spitze`` bei eine Warnung und liefert ein falsches Ergebnis.

In[1]:=NIntegrate[Exp[-xx{2],,-1000,1000},
MinRecursion->3, MaxRecursion->10]

löst das Problem.

Maple:

>int(f,x=a..b);

liefert, wenn möglich, eine symbolische Lösung des Integrals.
 
Für Mehrfachintegrale verwendet man int entsprechend oft verschachtelt.
 
Numerische Integration, erreicht man durch Voranstellen des Befehls evalf mit der Genauigkeit von n Ziffern:

>evalf(int(f(x),x=a..b),n);

>readlib(` evalf/int`): , Bibliotheksaufruf zur Verwendung eines adaptiven Newtonverfahrens.

>` evalfint`(exp(-x_NCrule2),x=-1000..1000,10,);
1.772453851

Das dritte Argument gibt die Genauigkeit, das letzte die interne Bezeichnung des Näherungsverfahrens an.

Differentialgleichungen:

Mathematica: Symbolische Behandlung, wenn eine Lösung in geschlossener Form möglich ist. Anweisungen:

NDSolve[ Dgl,y,{x,xa,xb}]

liefert eine numerische Lösung der Differentialgleichung im Bereich zwischen und .
 
Lösung der Gleichung für das Foucaultsche Pendel:

In[1]:=dg=NDSolve[{x''[t]==-x[t]=-x[t]+0.05y'[t],

y''[t]=-y[t]-

0.05x'[t],x[0]==0,y[0]==10,x'[0]==y'[0]==0},

{x,y},{t,0,40}]

Out[1]={{x->InterpolatingFunction[{0.,40.},<>],

y->InterpolatingFunction[{0.,40.},<>]}}

Mit

In[2]:=ParametricPlot{x[t],y[t]}/.dg,t,0,40,

AspectRatio->1]

stellt man die Lösung dar.
 
Maple:

>dsolve( Dgl, y(x));

löst Differentialgleichungen und Systeme symbolisch. Als letztes Argument ist eine Option erlaubt:

 
Lösung mit Anfangsbedingungen:

>dsolve({diff(y(x),x)-exp(x)-y(x)^}2,y(0)=0,y(x),
series);

 
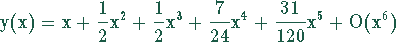
Auch bei der Option numeric enthält die Anweisung die Anfangsbedingungen. Zur Berechnung der Lösung wird das Runge-Kutta-Verfahren verwendet.