|
|
|
|
|
|
|
|
Integrale, die analytisch nur schwer oder gar nicht zu lösen sind, können numerisch durch eine Aufspaltung des Integrals in eine endliche Summe berechnet werden:
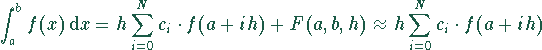
mit verfahrensabhängigen Konstanten 
und
ist der Fehler der Näherung.
N ist die Anzahl der Unterteilungen des Intervalles,
h die Breite der Intervalle.
Je größer N,
um so besser ist die Näherung, desto länger ist die Rechenzeit.
Bei zu feiner Unterteilung (zu großem N) können Rundungsfehler
das Ergebnis verfälschen.
Man vergrößere die Anzahl der Unterteilung N so lange,
bis sich der Wert des
Integrals innerhalb der signifikanten Stellen nicht
mehr ändert:
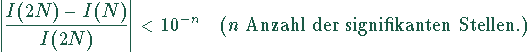
n darf nicht über der Stellenzahl des verwendeten Datentyps liegen
(einfach-genau: 
, doppelt-genau: 
).
Die Güte der Näherung für ein bestimmtes Integral hängt ab
von
1. der Fehlerordnung 
,
2. der Feinheit der Zerlegung h,
3. der Glattheit des Integranden.
|
|
|
|
|
|
|
|
