|
|
|
|
|
|
|
|
schließen, daß das Vektorfeld
sich als Rotation eines Vektorfeldes 
schreiben
läßt.
Für 
wird gefordert, daß 
ist (reines
Wirbelfeld). Es gilt dann
was wieder zu einer Poisson-Gleichung für die Vektorkomponenten von
führt. Eine Lösung hierzu ist
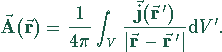
Die Lösung zu den Randbedingungen erhält man durch die Überlagerung
mit einem entsprechenden wirbel- und quellenfreien Feld U.
Das Feld 
erhält man durch
.
|
|
|
|
|
|
|
|
