|
|
|
|
|
|
|
|
im Grundbereich G eine
Fuzzy-Menge:
Fuzzy-Relation: Eine unscharfe Relation R in G ist eine unscharfe
Teilmenge R:
.
R läßt sich beschreiben durch eine Zugehörigkeitsfunktion 
,
die jedem Element 
den Zugehörigkeitsgrad 
aus 
zuordnet.
Eine Kreuzproduktmenge aus n Grundmengen heißt n-stellige
Fuzzy-Relation.
Folge: Die bisher betrachteten Fuzzy-Mengen waren
einstellige Fuzzy-Relationen, d.h. Kennlinien über einer Grundmenge. Eine
zweistellige Fuzzy-Relation kann als Fläche über G interpretiert werden.
Diskrete endliche Grundmengen: Darstellung der zweistelligen
Fuzzy-Relation als Fuzzy-Relationsmatrix.
Farbe-Reifegrad-Relation: Modellierung des bekannten
Zusammenhangs in Form einer Relationsmatrix zwischen Farbe x und Reifegrad
y einer Frucht mit den möglichen Farben 
{grün, gelb, rot} und
Reifegrade 
{unreif, halbreif, reif}.
Als binäre Relationsmatrix mit Elementen aus 
:
also
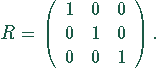
Interpretation:
Als Fuzzy-Relationsmatrix mit 
(grün,
unreif) 
;
(grün, halbreif) 
; 
(grün,
reif) 
; 
(gelb, unreif) 
;
(gelb, halbreif) 
;
(gelb, unreif) 
;
(rot, unreif) 
;
(rot, halbreif) 
; 
(rot, reif) 
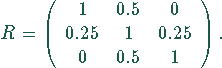
Rechenregel für die Verknüpfung von
Fuzzy-Mengen z.B. 
und 
auf unterschiedlichen Grundmengen mit der
UND-Verknüpfung, d.h. dem MIN-Operator:
Interpretation: Das Ergebnis der
Verknüpfung ist eine Fuzzy-Relation R auf der Kreuzproduktmenge G mit
.
Kreuzprodukt oder kartesisches Produkt der Fuzzy-Mengen. Sind
X und Y diskrete Mengen und somit 
als Vektoren
darstellbar, so gilt
Verknüpfungsoperator 
steht nicht für das übliche
Matrizenprodukt, die Produktbildung wird durch die MIN-Operation und die
Addition durch den MAX-Operator ersetzt.
Interpretation: Der Grad des Zutreffens einer inversen
Relation 
auf die Objekte 
ist also stets gleich dem Grad des
Zutreffens von R auf die Objekte 
.
|
|
|
|
|
|
|
|
