|
|
|
|
|
|
|
|
Grenzverteilungsfunktion, Grenzverteilung, Grenzwert einer Folge von Verteilungsfunktionen.
Verteilungsfunktion einer normalverteilten Zufallsgröße ist
Grenzverteilungsfunktion einer Folge binomialverteilter Zufallsgrößen.
Grenzwertsatz von Poisson, Zusammenhang von Binomial- und
Poissonverteilung; Aussage über das Grenzverhalten der
Einzelwahrscheinlichkeiten binomialverteilter Zufallsgrößen für große
n und kleine p als Poissonverteilung:
Näherung praktisch bedeutungsvoll durch Verringerung des
Rechenaufwandes bei der Berechnung binomialverteilter Zufallsgrößen
und nutzbar für 
und 
Zentraler Grenzwertsatz, Grenzwertsatz von Lindeberg-Levy:
Eine Zufallsgröße ist annähernd normalverteilt mit dem Erwartungswert
nm und der Varianz 
, wenn sie als Summe einer großen Anzahl
von stochastisch unabhängigen Zufallsgrößen aufgefaßt werden kann,
die alle der gleichen Verteilungsfunktion mit dem Erwartungswert m und
der Varianz 
genügen.
Grenzwertsatz von Ljapunow:
Eine Zufallsgröße Y ist annähernd normalverteilt mit den Parametern
und 
, wenn sie als
Summe einer großen Anzahl n unabhängiger Summanden (Zufallsgrößen
mit den Erwartungswerten 
und den Varianzen 
)
dargestellt werden kann, von denen jeder zur Summe einen unbedeutenden
Beitrag liefert.
Prüfen einer annähernd normalverteilten Zufallsgröße praktisch
durch Erkennen einer Geraden auf einem Wahrscheinlichkeitspapier
nach Eintragen der Stichprobenwerte, Anwenden eines Anpassungstests
der mathematischen Statistik.
Grenzwertsatz von Moivre-Laplace:
Bei einer großen Anzahl unabhängiger Versuche (durchgeführt nach dem Bernoullischen Versuchsschema) konvergiert die Verteilungsfunktion der standardisierten binomialverteilten Zufallsgröße stochastich gegen die Verteilungsfunktion der standardisierten Normalverteilung (globale Aussage):
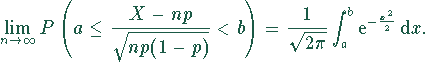
Lokale Aussage (vereinfacht): Einzelwahrscheinlichkeiten einer
Binomialverteilung mit den Parametern n und p konvergieren gegen
die entsprechenden Werte der Dichtefunktion 
einer
Normalverteilung mit den Parametern 
und 
:
Während der Grenzwertsatz von Poisson nur für kleine Werte p
eine gute Annäherung der Einzelwahrscheinlichkeiten binomialverteilter
Zufallsgrößen liefert, kann nach dem Grenzwertsatz von Moivre-Laplace
ihre Annäherung durch die Normalverteilung für jedes 
, und
hinreichend großem n erfolgen.
Faustregel für die Anwendbarkeit:
|
|
|
|
|
|
|
|
