|
|
|
|
|
|
|
|
bzw. 
und die
Konfidenzintervalle vorgegeben.
Aufgabe ist, den notwendigen Stichprobenumfang n
zu bestimmen, der gewährleistet, daß sich der Parameter W
wirklich mit mindestens der Wahrscheinlichkeit 
( Aussagesicherheit) in den Konfidenzgrenzen aufhält.
Genauigkeitsvorgabe, Angabe der Konfidenzgrenzen,
Vorgabe für die Abweichung 
, die mit der Wahrscheinlichkeit
von 
nicht überschritten wird.
Diese Angabe geschieht durch den absoluten oder relativen Schätzfehler
und ist unabhängig von der Vorgabe der Aussagesicherheit 
.
Die Genauigkeitsvorgabe ist neben der Aussagesicherheit eine
weitere Forderung.
Absoluter/relativer Schätzfehler 
,
Wert bzw. relativer Wert der Abweichung 
.
Forderungen an den Erwartungswert 
( heterograde Untersuchung),
sind die Aussagesicherheit 
sowie die Genauigkeitsgrenzen durch v oder 
vorgegeben, ergeben sich folgende
Bedingungen, nach denen der Stichprobenumfang n ausgewählt
werden muß:
Dies ist bei Normalverteilung gleichbedeutend mit
und damit muß für n gelten
Die entsprechenden Bedingungen bei Vorgabe von 
sind gleich, wenn man v durch 
ersetzt (
oder 
).
Forderungen an den Anteilparameter p
( homograde Untersuchung),
sind die Aussagesicherheit 
sowie die Genauigkeitsgrenzen durch v oder 
vorgegeben, ergeben sich folgende
Bedingungen, nach denen der Stichprobenumfang n ausgewählt
werden muß:
Dies ist bei Binomialverteilung gleichbedeutend mit
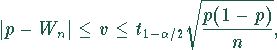
und damit muß für n gelten
Natürlich gelten diese Ungleichungen ebenso für
die hypergeometrische Verteilung.
Die Größen
und t müssen jedoch wie
angegeben ersetzt werden!
Die entsprechenden Bedingungen bei Vorgabe von 
sind gleich, wenn v durch 
ersetzt (
oder 
)
wird.
|
|
|
|
|
|
|
|
